By

文章目录
  1. 1. What is Overfitting
  2. 2. The Role of Noise and Data Size
  3. 3. Solution for Overfitting
  4. 4. 参考

What is Overfitting

假设现在我们使用一个二次函数随机产生几个点，并且加入非常少量的噪声，然后使用一个四次函数来进行拟合
将得到如下的结果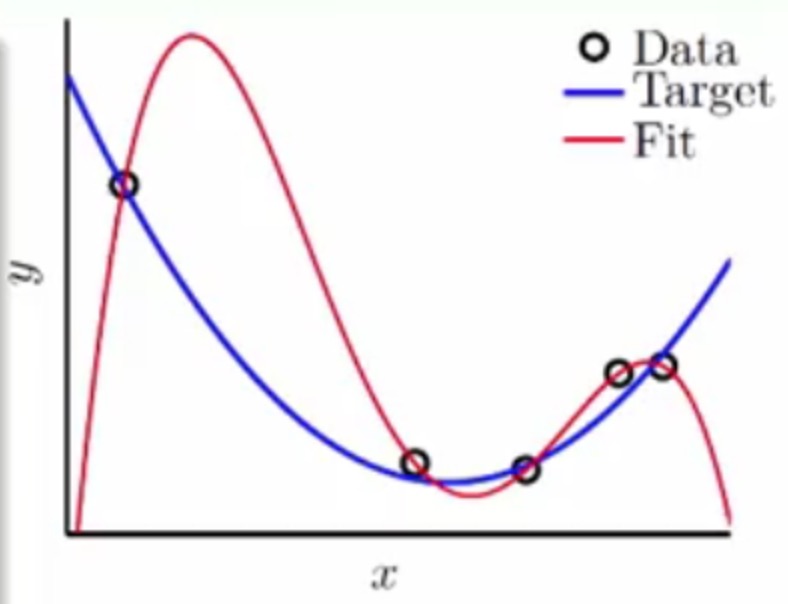

可以发现4次函数可以完全拟合含有噪声的2次函数产生的点，也就是拟合出来的Ein=0，但是此时如果使用新的2次函数的点用这个4次的拟合函数来进行预测的话，可以发现Eout会很高，
这种低Ein高Eout就是叫做泛化能力差(BAD generalization)，也是往往我们在做训练预测时不希望看到的。

此时再来回顾一下VC维中经典的一张图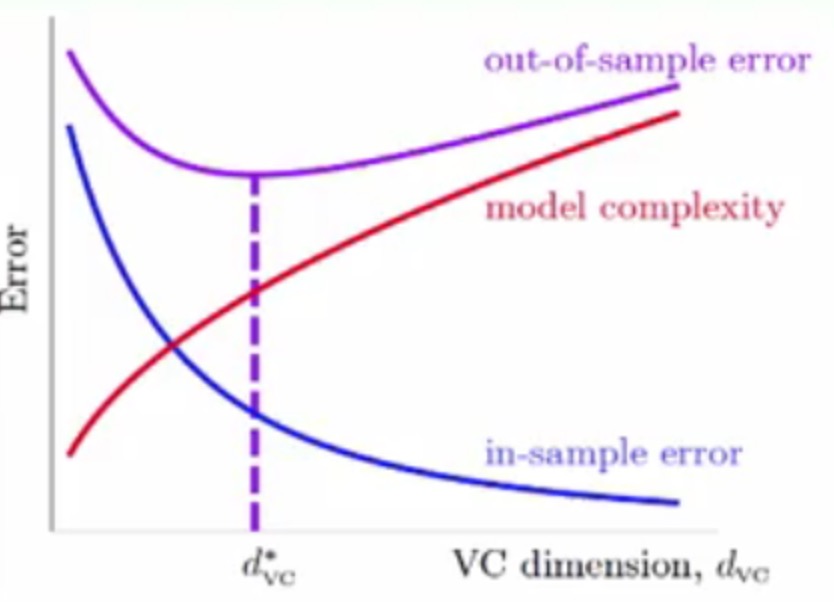

可以看到VC维在d*vc的时候可以有最小的Eout
但是在d*vc的右侧，可以发现VC维在不断增大时，Ein不断减小，但是Eout会不断增大，这种就是过拟合了（Overfitting）

其实在d*vc的左侧叫做欠拟合underfitting，这种情况一般通过增加特征或者向高维映射来进行解决，但是Overfitting是由于一般是VC维太大造成的，不容易解决

Overfitting产生的主要原因有

  1. 使用了太多的VC维，也就是模型太复杂了（类似刚刚用4次方的线）
  2. 噪声Nosie太多，这些噪声都被训练函数给拟合学习了
  3. 数据量太少

The Role of Noise and Data Size

以二维平面上的函数为例，现在平面上有这么一些点：

  1. 一种是以十次多项式产生的点，但是加上了一些噪声
  2. 另一种时以五十次多项式产生的店，但是没有噪声


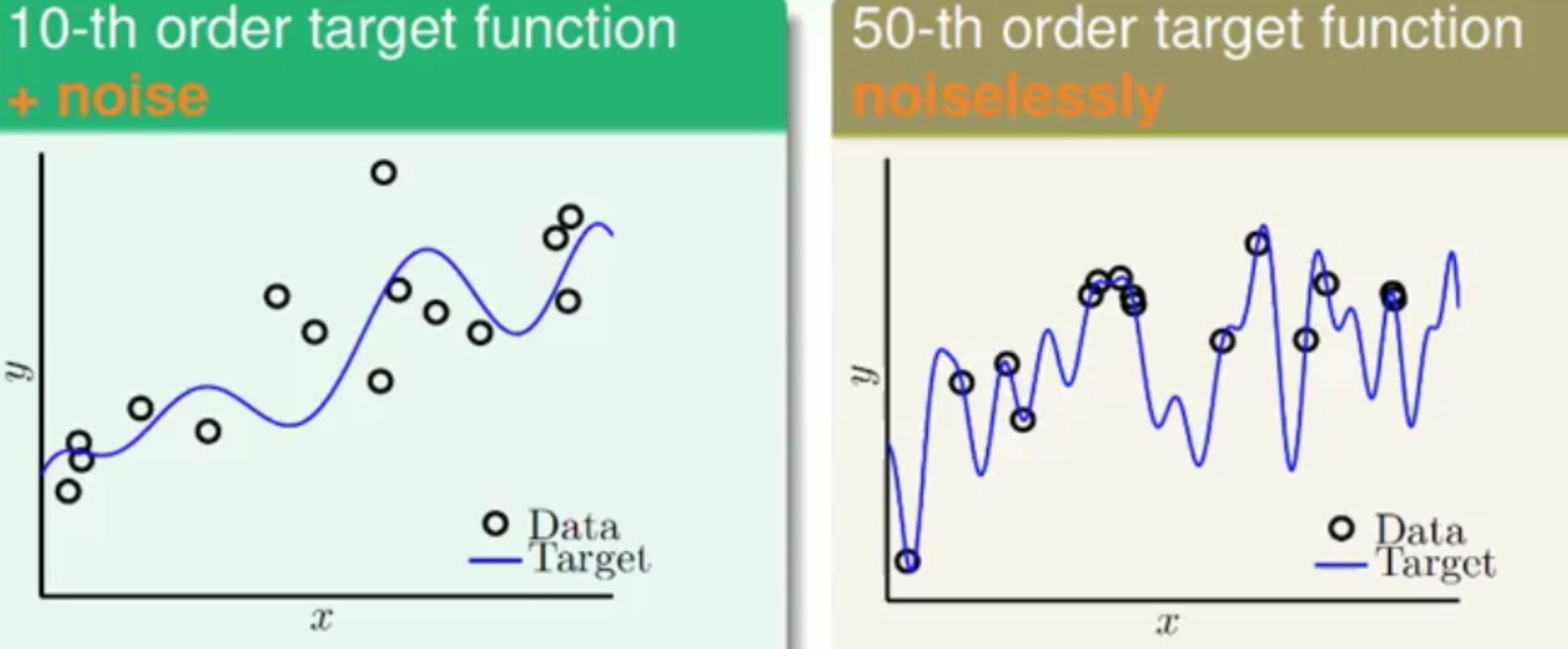
分别使用一个二次多项式(H2)和一个十次多项式H10用回归的方式去拟合这两个平面上的点

最终拟合得结果为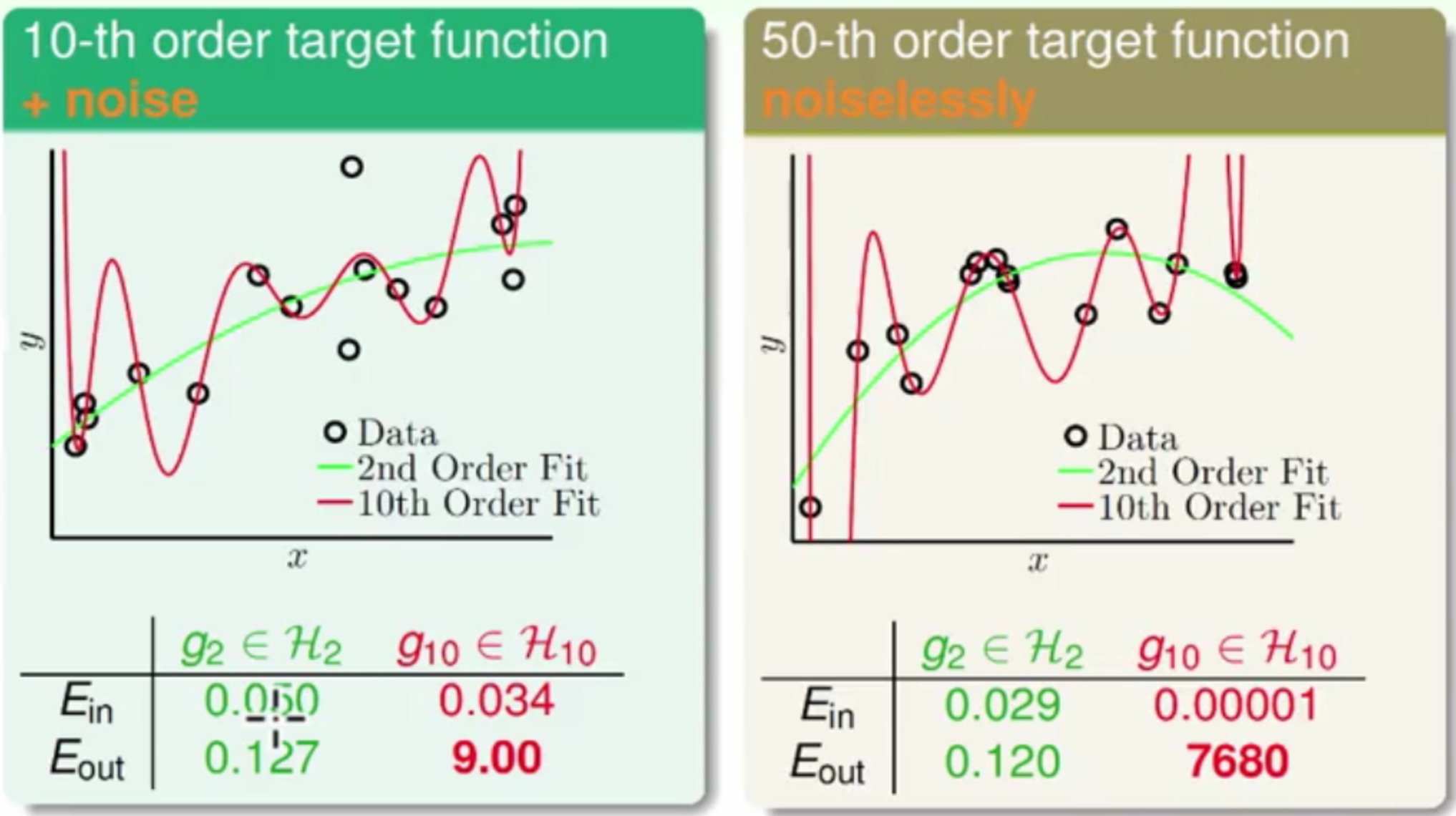

从两个平面上均可以惊奇的发现：

  • H2的Ein比H10的大，但是在Eout却比H10小的多
  • H10的Ein可以做到很小，但是观察图H10在图上的高低之处正好与原图相反

也就是说从H2切换到H10时，Ein变小了，但是Eout增加了，也就是此时发生了Overfitting

这里比较有意思的是原来是十次项产生的点用十次项的线来拟合，该Eout竟然比二次项的线要高很多-_-，这是为何呢？？

可以看看这两个多项式的学习曲线（这个是针对Liner Regression）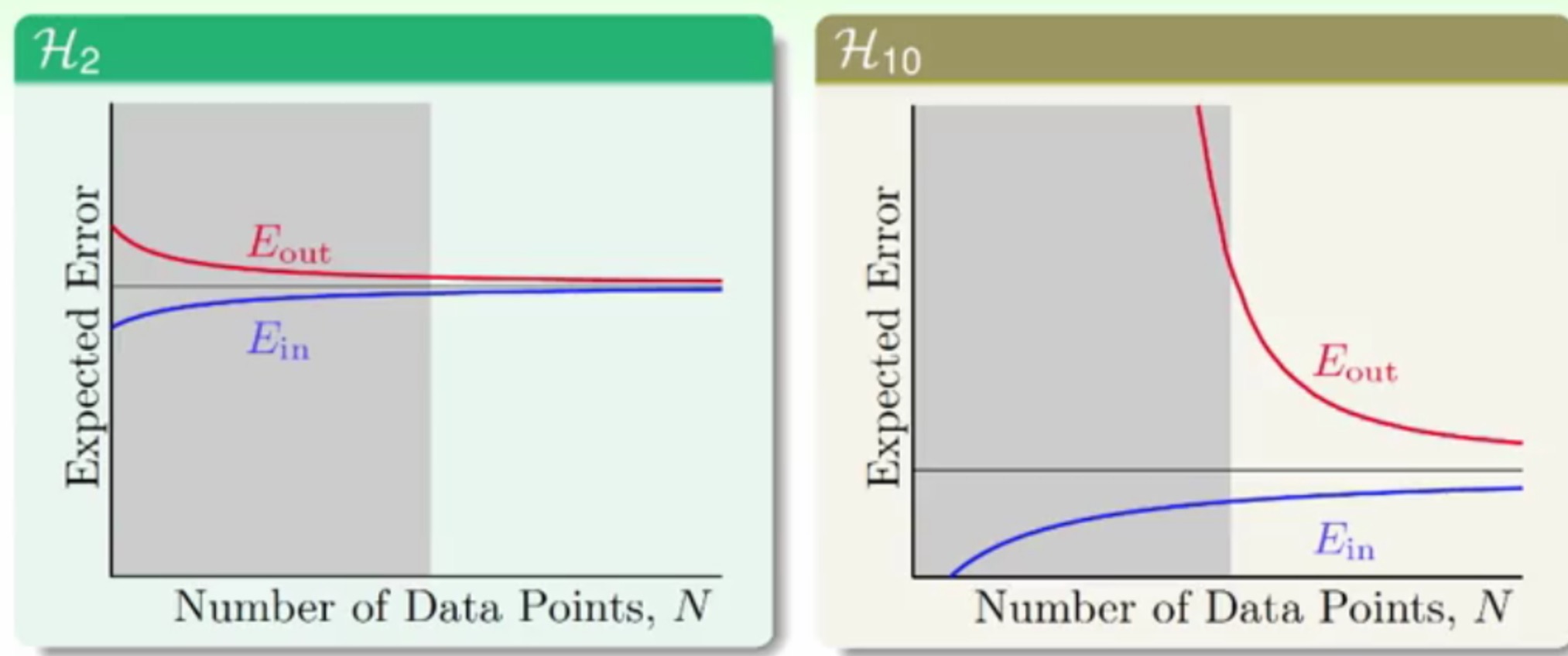

其中：

  1. 当样本量无限多的时候，Ein会接近于Eout，否在在有限样本时，Ein总小于Eout，因为训练出来的线总是往训练样本靠拢，这样在预测样本上的时候这个靠拢的距离就会变大。
  2. 随着样本量的增加，Ein会慢慢增加，但是Eout会慢慢减少
  3. 当样本量较少的时候(也就是左边的区域)，这里随着Ein的减少，Eout会增加，也就是出现了Overfitting的情况，应该就是出现了Overfitting的情况，只是左侧的图(十次多项式)更加明显而已

所以啊，可以看出使用简单的模型有多重要^_^

这里再来进一步进行一些Overfitting的实验
现在有一个多项次函数和高斯噪声产生的点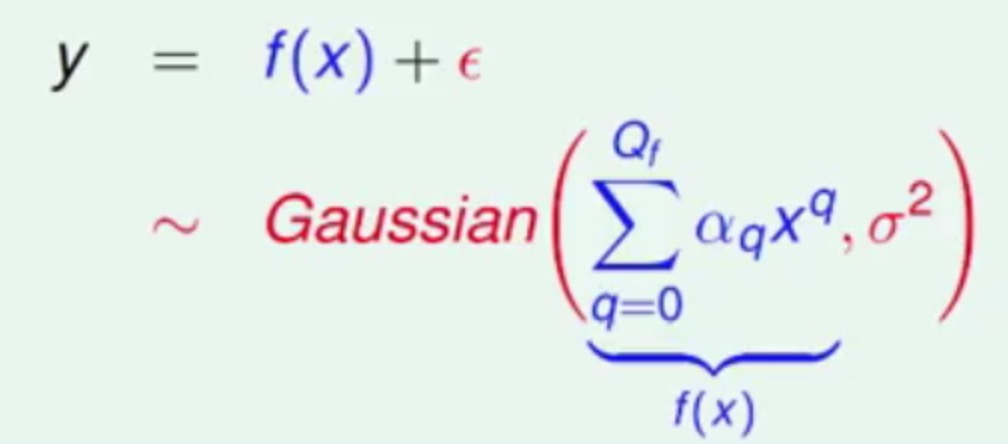

有三个参数：

  1. σ2表示高斯噪声的强度
  2. Qf表示目标多项次函数的复杂度(比如50次多项式 就是Qf=50)
  3. N表示训练数据量的大小

还是用H2(g2)和H10(g10)进行实验，根据上一个实验的经验，这里肯定成立的是Ein(g10)<Ein(g2),现在设定Overfitting的度量为Eout(g10)-Eout(g2)，如果这个差值越大，说明Overfitting得越厉害。

那这样直接看实验结果图

这里横纵坐标是用上面三个参数中选的，还有平面上的颜色表示Overfitting的程度，也就是右侧的那个小纵条，越往上升，Overfitting得越厉害（度量的差值越大）。

先来看噪声强度σ2和样本数量N对Overfitting的影响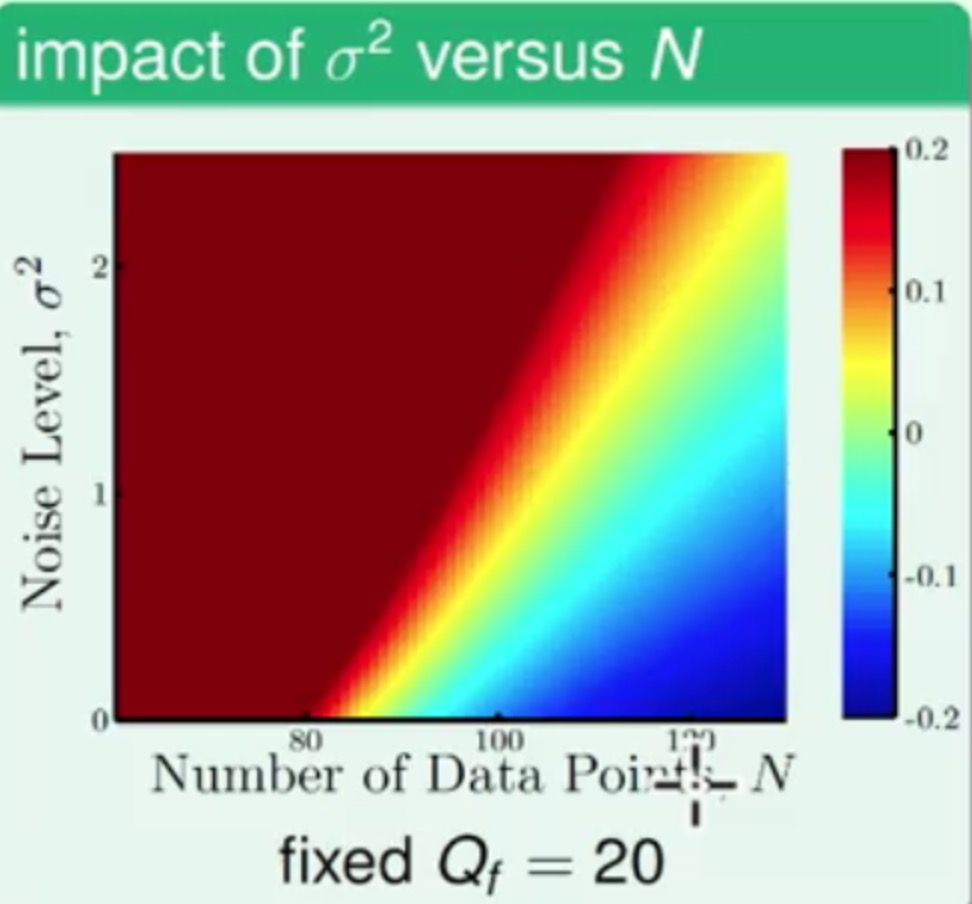

从图中可以看到：

  • 样本数量越少，噪声强度越大的时候，Overfitting得越厉害
  • 样本数量越多，噪声强度越小的时候，Overfitting的程度很轻

    恩，这想想也是，结果挺合理的^_^

再来看看一张比较扭曲的图：目标多项次函数的复杂度Qf和样本数量N对Overfitting的影响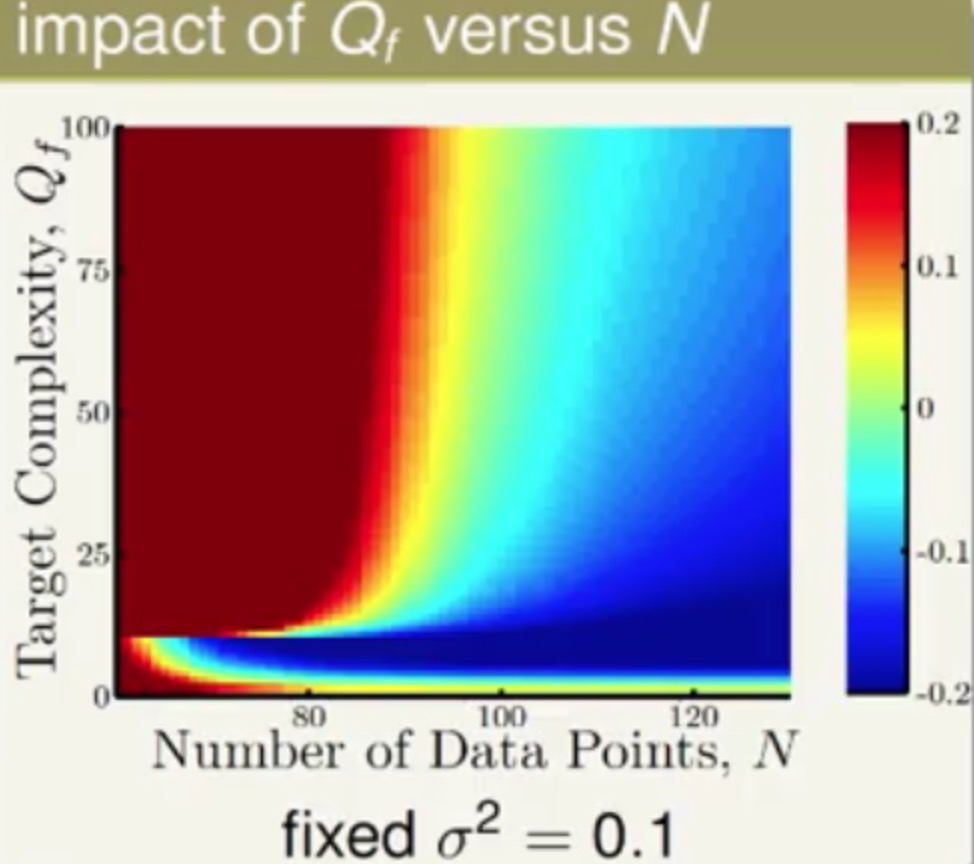

其实这张图大致上和上面的趋势是一直的，只不过在较少样本同时在较小的复杂度情况下也可以得到较小的Overfitting。

额。。。这个原因我也不是很了解，先去问问其他大神！！

上面两个图中的纵坐标中：

  1. 高斯噪声也叫做随机噪声(stochastic noise)
  2. 目标的复杂度也叫做确定性噪声(deterministic nosie)
    这个怎么说呢，比如一个十次项的目标函数产生的点，用一个二次项来拟合，那么这些点中必定有一些是在二次项之外的，那这不就是噪声了嘛，所以这个噪声是可以计算出来的

他们俩都会对Overfitting都会有影响，并且影响都很类似，不过差别就是deterministic nosie和训练的模型是有改关的。

Solution for Overfitting

既然了解了Overfitting出现的原因以及导致的后果，那咱们该如何处理呢？大致有以下几种方法

  1. 使用简单的模型
    根据之前VC维的理论，简单的模型VC维较低，可以得到较低的Eint
  2. 剪枝或者数据清洗
    其实是为了降低噪声带来的影响
  3. 数据的提示
    在原特征上再挖掘有用特征，这样可以弥补训练样本少带来的问题
  4. 正则项
    额。好东西，不过下个视频才讲-_-
  5. 验证
    应该可以理解为交叉验证把？

参考

  • 《台湾国立大学-机器学习基石》第十三讲

配图均来自《台湾国立大学-机器学习基石》

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。

文章目录
  1. 1. What is Overfitting
  2. 2. The Role of Noise and Data Size
  3. 3. Solution for Overfitting
  4. 4. 参考